6. Maths Trigonometry

Trigonometry is based on triangles. The point of trigonometry is to find either the unknown side or angle of a triangle, when we know a side and an angle.

Here is a little diagram to get you started (pretty isnt it).

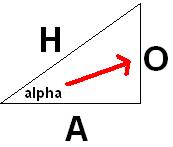
Now:
O stands for opposite.
A stands for adjacent.
H stands for hypotenuse.
alpha is the angle in the corner where the angle is either known, or needed to be found.

Ok, now the 3 trigonomic functions are:
Sine, Cosine and Tangent

These will be known as:
sin, cos and tan on your calculator.

And respectively they each have their own inverse function known as:

sin^-1, cos^-1 and tan^-1

Here I am going to let alpha be @ as I dont have any alpha key to press 😛
so to remind you alpha is our angle, so @ will be known now as our angle.

Now the
sin@ = o/h
cos@ = a/h
tan@ = o/a

You can easily remember this by a little saying:
soh cah toa

So why do we need this? We need this when we want to find the length of a side in a triangle. If you have the length A and the angle @, then you can use trigonometry to find either H or O. And likewise for the lengths H and O.

Next we can use trigonometry to find the unknown angle.

To do this, you start with your basic formula, eg:
sin@ = o/h

Then we have to get sin on the other side, so we times both sides by the opposite
of sine which is sin^-1, which should also be on your calculator.

so by doing this we end up with:

@ = sin^-1(o/h)

And that is all there is to trigonometry. You can find the sides and angles of a triangle using this.

But how would we use this in a game you might say, well take a little look at my next diagram (god I love mspaint).

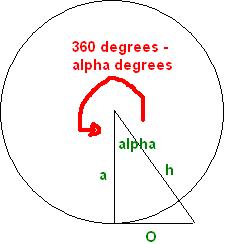
In the image above it shows you a rough idea of how you would make this into a camera for a game. You have yourself in the centre and have 360 degrees of rotation around. You can use trigonometry, and with your current angle, and knowing your current position to A(where you wish to go) you can determine your point at the corner of H and O.

But that is just a quick reference I whipped up in 10 minutes. In the Radian tutorial you will find out just how the camera class relates to trigonometry in detail.

If you have any questions, please email me at swiftless@gmail.com