2. Maths Pythagoras Theorem
Posted on : 25-03-2010 | By : Swiftless | In : Maths
Tags: formula, Maths, pythagoras, tutorial
2
Most people who have done maths in high school, would have heard of Pythagoras theorem.
This is used to work out the unknown side of a triangle, if you know the other 2 sides.
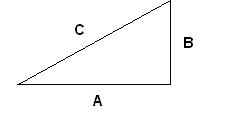
Here you can see the sides, A, B and C.
Now Pythagoras theorem states that A^2 + B^2 = C^2
So if you know any two sides, you add them in, rearrange the formula if needed, and then you can solve for the unkown sides.
So how would you use this in a game? What about collision detection? Using this you can find quite easily in a 2 dimensional plane when 2 points will meet.
They will meet when A^2 + B^2 = 0
Quite simple really, you take the position of A and B on the X axis and do the equation, then if it comes up with an answer of 0, you then take the position of A and B on the Y axis, then if that also comes to 0, they must be colliding.
So to put that in other words, we are finding the distance 
If the distance is nothing, then they are located in the same position.
Not sure if that is right, sounds right from my position, although it is 1:18 am.
If you have any questions, please email me at swiftless@gmail.com
Related posts:
Loading ...
Hi Flekken,
That is exactly true, A^2 + B^2 will only equal 0 if A and B is 0.
While the formula you have given is the true formula for working out the distance between two points, look at what it is actually doing. I will look at 2D space:
Now if we have a collision when the result is 0, if we apply some basic maths to the distance formula, we can remove the sqrt:
0 = sqrt((x2-x1)^2 + (y2-y1)^2)
0^2 = sqrt((x2 – x1)^2 + (y2 – y1)^2)^2
0 = (x2 – x1)^2 + (y2 – y1)^2
And now look at what x2-x1 and y2-y1 do. They give us the length of the line segments A and B.
Therefore:
x2 – x1 = A and y2 – y1 = B
And then:
0 = (A)^2 + (B)^2
0 = A^2 + B^2
Therefore we have a collision. Both this shorthand version and the full version of the distance formula are the same thing.
Hope this helps clarify
Swiftless
I don’t understand how can you use this for calculating distance. The only time A^2 + B^2 would be 0 is when A and B is 0. The proper formula for calculating distance between 2 point is:
sqrt( (x2-x1)^2 + (y2-y1)^2 + (z2-z1)^2 )